2018年1月21日更新
【研究】-【磁気抵抗】
磁気抵抗とは物質の電気抵抗は温度や圧力で変化しますが,外部から磁場を印加することでも変化します.これを磁気抵抗効果と呼びます.また,磁場がないときと比較した電気抵抗の増加率ΔR/Rを,慣用的に磁気抵抗といったりもします.実験的には,通常の金属の磁気抵抗は,低磁場では磁場強度の二乗に比例して大きくなることが知られています.磁気抵抗効果は,固体中の自由電子が磁場で進路を曲げられるために起こります.金属に電流を流すために電圧をかけたとします.自由電子は電圧のかかっている向きに加速されますが,さらに磁場が加わると,磁場に垂直な向きに曲がる力を受けます.これをローレンツ力といいます.固体中に無数にある自由電子は互いに異なる速度(大きさと向き)を持っていて,ローレンツ力の受け方も異なります.進路を曲げられる効果を自由電子全体で平均すると,電気抵抗が磁場の二乗に比例して増大するという実験結果を説明することができます. 磁場の強さにもよりますが,室温では普通の金属の磁気抵抗はほとんどゼロです.これは電子が格子振動によって頻繁に散乱されているので,磁場によって進路が曲がる効果が現れにくいためです.しかし,液体ヘリウム温度(4.2 K)やそれ以下の低温では格子振動が抑えられるために,しばしば,ΔR/R = 1 – 1000といった非常に大きい磁気抵抗が観測されます.このため,磁気抵抗の研究は通常低温で行います. 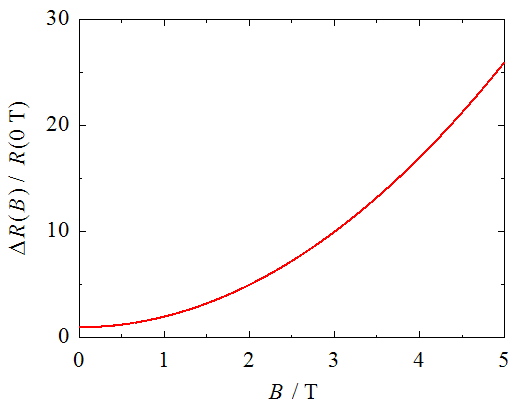 図1 通常の磁気抵抗の磁場依存性.横軸の単位は[T(テスラ)]. シュブニコフ–ド・ハース効果金属の特徴はフェルミ面を持つことです.フェルミ面は,その金属中で最高のエネルギーを持つ電子の波数ベクトルの分布に相当します.自由電子モデルでは,三次元の場合は球殻状(図2(a)),二次元の場合は円筒状(図2(b))ですが,実在金属では元素や結晶構造の違いに応じて,フェルミ面も異なる形をしています.磁気抵抗を測定する目的の1つは,物質のフェルミ面の形状を明らかにすることです.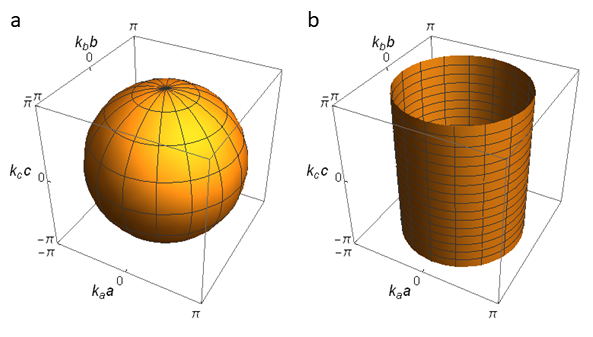 図2 (a) 三次元自由電子のフェルミ面.(b) 二次元自由電子のフェルミ面. フェルミ面研究の有効な手段としてシュブニコフ–ド・ハース効果が知られています.これは磁気抵抗が磁場強度の逆数に対して周期的に振動する現象です. 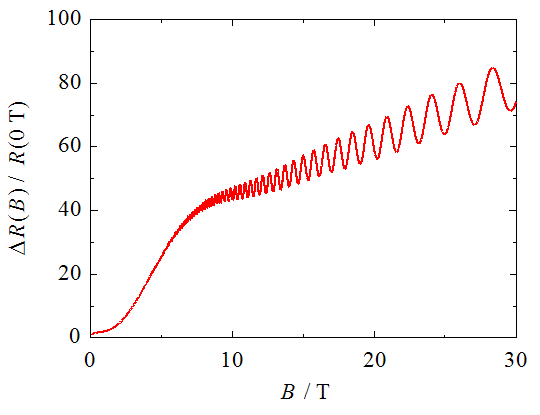 図3 磁気抵抗の振動現象の一種であるシュブニコフ–ド・ハース効果の例. この振動は,磁場Bではなく磁場の逆数(1/B)に対して周期的なことがわかっています.図3の磁気抵抗をを,1/Bに対してプロットしたのが図4です. 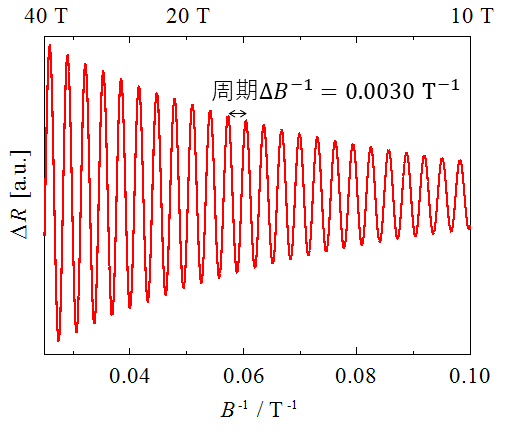 図4 図3の磁気抵抗の振動成分を1/Bに対してプロットしたグラフ.a.u.はarbitrary unit(任意単位)といって,絶対値に意味がないときに使う. 振動の山の高さは変化していますが,周期=山と山の間隔が図4ではほぼ一定になっていることがわかります.周期は0.0030 T-1と読み取ることができます.単位がT(テスラ)の逆数になっていることに注意してください.周期の逆数を振動数といいます.これをFとすると,今の場合F = 3.3×102 T(再び単位に注意)です. 理論によればFとフェルミ面の磁場に垂直な断面積SFは比例します. ここで,eは電荷素量,ℏはプランク定数を2πで割ったものです. ところで図5に示すように,Fermi面の磁場Bに垂直な断面はいくつもあることがわかります. 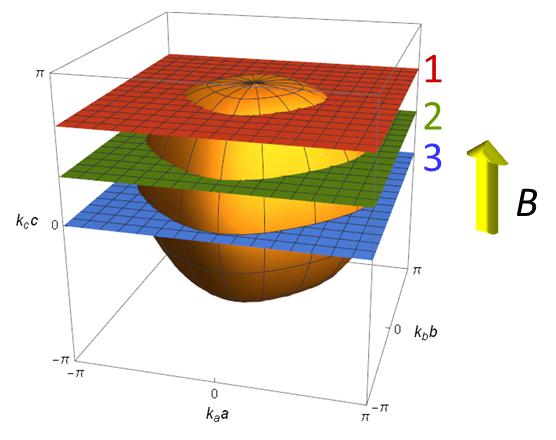 図5 フェルミ面の磁場Bに垂直な異なる断面. それぞれの断面積が異なりますから,異なる振動数Fの磁気抵抗振動を与えます.しかし,SFが極大値をとる3の平面とフェルミ面の交差する周上に属する電子の数が最も多いので,実際には3の断面積に比例する振動が観測されます.すなわち,シュブニコフ–ド・ハース効果でわかるのはフェルミ面の磁場方向の極値断面積です.これだけでは,三次元的な形状はわかりませんが,いろいろな方向から見たときの極値断面積の大きさを知ることで,図6のような単純な球や円筒状でない実在物質のフェルミ面の形状も推定することができます. 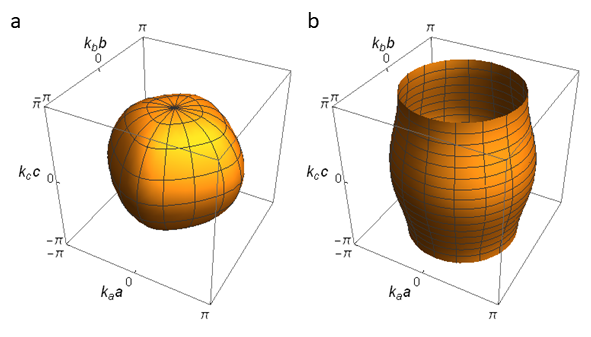 図6 (a) 実在金属類似のフェルミ面,(b) 擬二次元電子系のフェルミ面. さて,シュブニコフ–ド・ハース効果の起源ですが,これは自由電子が磁場中で回転運動をすることと関係しています.これをサイクロトロン運動といいます.素粒子である電子は粒子であると同時に波としても振る舞います.波の性質すなわち波動性はサイクロトロン運動にも現れます.電子が磁場中で一回転する軌道の長さは,電子波の波長の整数倍でないといけません(図7(a)).そうでない電子波(図7(b))は,自分自身との干渉で山と山,谷と谷が一致しないので存在できません.サイクロトロン運動の軌道長が波長の整数倍に限定されることをランダウ量子化といいます. 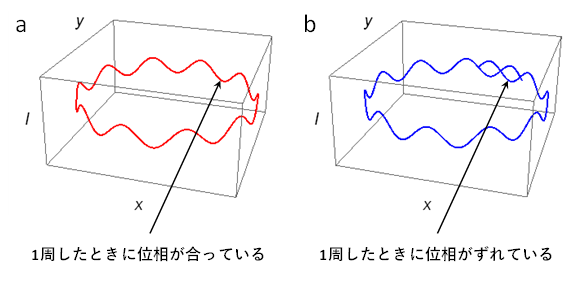 この量子化のために,磁場強度を変化させたときにフェルミ面の電子の数が振動的に変化することになります.これが磁気抵抗の振動となって観測されるのです. 擬一次元的フェルミ面と磁気抵抗シュブニコフ–ド・ハース効果はサイクロトロン運動のランダウ量子化を基に理解することができます.サイクロトロン運動は,フェルミ面の断面が閉じているときに起こりますので,三次元や二次元のフェルミ面では可能ですが,図8に示す一次元や擬一次元的なフェルミ面では起こりません.一次元フェルミ面は2対のシート状です.フェルミ面は,波数ベクトルkで表した空間における電子の等エネルギー面なので,各電子はフェルミ面に垂直な法線の向きに走っています.したがって,各シート上の電子は全て同じ向きに走っていますので,このようなフェルミ面を持つ物質があれば,この向きにしか電流が流れないということになります.この方向を一次元軸といったりします.実際は一次元軸に垂直な方向にも,わずかながら電子は運動していますので,異方性の |
