2014年1月7日更新
【研究】-【輸送現象】
|
ここで紹介する「輸送現象」とは,電荷や熱が固体中を伝わることで,電気伝導,熱伝導,熱電気現象などを指します. 【電気抵抗率ρ/電気伝導度σ】 電荷の流れが電流です.例えば,乾電池と豆電球を金属線を使ってつなぐと,電流が乾電池の+極から-極に流れます.この電流を流す力は,電圧や起電力と呼ばれます.電流(電気の流れ)を担っているのは,普通は電子(自由電子)です.金属の中には原子核に強く結合している内殻電子と,結晶中に広がって運動できる自由電子が存在します.この自由電子が乾電池の起電力によって運動することで,電流となっています. 豆電球の中にあるフィラメントは細くて電気の流れにくい金属でできているので,電子が通るときの抵抗(摩擦)が大きくなっています.このときに電子の運動エネルギーは摩擦熱となって失われます.この熱が蓄積してフィラメントの温度が高くなると豆電球が明るく輝きます. リード線は摩擦が小さく,フィラメントは摩擦が大きいという違いがあります.この摩擦のことを電気抵抗Rと呼びます.電流Iと電圧Vの間には,オームの法則として知られる比例関係があります. この式は,乾電池を増やすなどして電圧を2倍,3倍にすれば,電流も2倍,3倍になることを意味しており,その比例係数がRです.輸送現象の比例係数なので,Rを輸送係数と呼んだりもします. リード線のRは小さく,フィラメントのRは大きいのですが,Rの大小には,材質だけでなく形状も関係しています.例えば,円柱状の金属に図のように電流が流れている場合,この金属のRは長さLに比例し,断面積Sに反比例することが知られています. 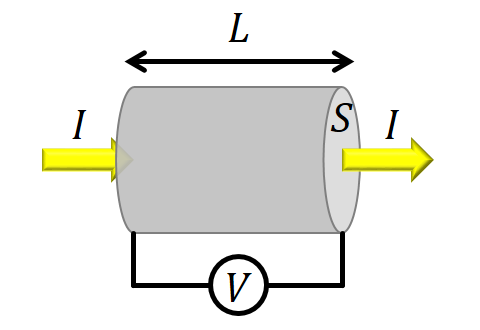 この比例係数ρを電気抵抗率と呼びます.上の式をρについて書き直してみます. Rは電流と電圧から決まり,SとLは円柱の形状を測ればわかります.これらを使えρを決めることができます.また,この式よりρは,電流が単位面積(例 S = 1 cm2)を単位長さ(例 L = 1 cm)にわたった流れるときのRに等しいこともわかります. このようにして決定したρは,同じ物質について同じ条件(温度,圧力,結晶性のよさ等々)で測定すれば,常に同じ値を持ちます.このように物質ごとに固有の値を示す物性を物質固有量と呼びます.ρはその物質が電流をどの程度流しにくいかを示す物量なので,その逆数である, は,その物質がどれだけ電流を流しやすいかを表す物量となります.σを電気伝導度と呼びます.ρやσは,最も基本的な輸送係数であり,私たちのグループが新物質の物性測定を行うときに,まず最初に決定する重要なものです. 【熱伝導度κ】 1秒ごとに流れる電荷が電流I ですが,1秒ごとに流れる熱を熱流 と呼ぶことにします.さらに単位面積あたりの熱流を熱流密度 と定義します.電流は印加した電圧に比例するというのがオームの法則でしたが,熱流密度が温度勾配∇T に比例することをフーリエの法則と呼びます.その比例係数が熱伝導度κで,やはり輸送係数のひとつです. 右辺の負号は,熱流(密度)の向きを正にとったときに,温度勾配が負であることと関係しています.下図は断面積S,長さLの円柱状固体の両端に温度差ΔTがあるときに,熱流 が流れているイメージです. 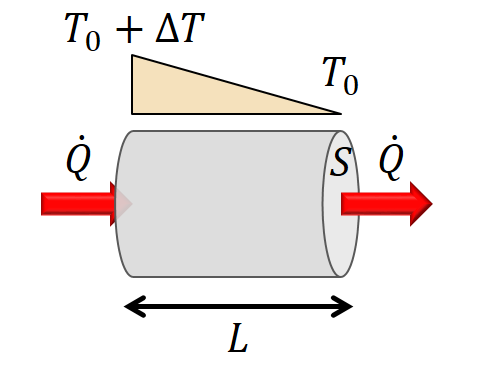 絶縁体結晶の場合,熱は格子振動の拡散によって伝えられます.一方,通常の金属では電子による熱輸送が支配的で,同じ温度ではκ は金属の種類が異なっても電気伝導度σ におおむね比例します.これはウィーデマン-フランツ則として知られています. ここで,Tは絶対温度,L0はウィーデマン-フランツ定数です.平たく言えば,「電気を伝えやすい金属は熱も伝えやすい」ということを意味しています. ウィーデマン-フランツ則は,電子がよく熱を伝える通常金属の場合はよく成り立ちますが,有機伝導体などのエキゾチック伝導体では電子よりも格子の方が熱をよく伝えるので,熱伝導度全体としては成り立ちません.逆に言えば,エキゾチック伝導体のκは電子系と格子系の両方の情報を含むので,電子系の情報を与えるσと比較することで,電子系に加えて格子系を理解するための情報も得られることになります.また,超伝導状態でのκは金属状態とは異なる温度依存性を示します.その挙動を理論と比較することで,エキゾチック伝導体の超伝導発現機構についても知見が得られます. ただし,電気物性と異なり,κの測定は一般に困難です.電気はリード線や試料だけを流れますが,熱は絶縁材や試料の周りの空気を伝わったり,電磁波の輻射を介して真空をも伝わるので,試料を流れる熱を正確に測定するのが難しいからです.私たちのグループでは,長さ1 mm以下の微小で脆い試料のκを定常比較法によって測定するシステムを開発し,測定法の改良にも取り組んでいます. 【熱電能S】 最後に電気と熱の両方が関係した熱電気現象について紹介します.下図のように2種類の異なる金属a, bを接続します.これを熱電対といいます.熱電対の開放端(左側)と接点(右側)の間に温度差ΔTがあると熱起電力ΔV という電圧が生じます.これをゼーベック効果と呼びます. 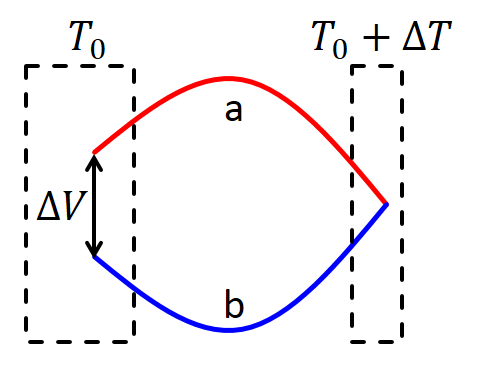 ΔT = 1 Kに対して,ΔV は通常10-6から10-4 Vと非常に小さいので,電力を取り出す役には立ちません.しかし,ΔVは金属a,bの長さや太さという形状には依存せず,金属の種類が決まればΔTだけに依存するという興味深い性質があります.例えば図のT0を0℃に固定して,ΔTを調節しながら変化させ,ΔVを測定すれば,ΔTとΔVの関係がわかります.この関係から逆に,温度がわからない物体に熱電対の接点を取り付けてΔVを測定してやれば,物体の温度(正確にはT0との温度差)を決定することができます. 熱電対には2種類の金属が必要です.それは,それぞれの金属が発生する熱起電力が異なり,その差が熱電対の熱起電力となるからです.温度差1 Kあたりの熱起電力を熱電能Sと呼びます. SはΔVとΔTの比例係数で,ゼーベック係数ともいいます.個々の物質の熱電能を絶対熱電能と呼びます.これも物質固有の輸送係数の一種です.例えば銅の絶対熱電能は正(300 Kで約2 μV K-1)です.銅と銅で熱電対を作ったとすると,互いの熱電能の差が全体の熱電能となるので,熱電能はゼロとなります.しかし,銅-コンスタンタンという熱電対の場合,コンスタンタンは負の絶対熱電能(300 Kで約-38 μV K-1)を持つので,熱電対全体の熱電能は,銅の正とコンスタンタンの負の熱電能の差の,(2-(-38)=40 μV K-1)となり,個々の熱電能よりも大きくなります.同じ温度差でも熱電能が大きい方がより正確に測定できますので,熱電能が正の金属と負の金属を組み合わせると温度計測に有利になります. 熱電対として利用される熱起電力/熱電能ですが,電気伝導体の電気物性研究の手段として熱電能Sは電気抵抗率ρの次によく測定される輸送係数です.それは,Sの符号が電流担体(キャリア)の種類に対応しているからです.よく知られているように,真性半導体の場合,0 Kでは価電子帯は電子で満たされており,伝導帯は空なので,電荷を運ぶ粒子がない絶縁体となります.しかし,有限温度では,少数の電子が価電子帯から伝導帯へバンド・ギャップを越えて熱励起されて,電気伝導性を帯びるようになります.このとき,電荷は伝導帯に励起された電子だけでなく,価電子帯に残された電子が空の状態である正孔(ホール)によっても運ばれます.正孔は+の電荷を持った粒子として振る舞うことから,このような名前がつけられています.真性半導体では,熱励起された電子と正孔の数は等しいのですが,p型やn型の不純物半導体では,それぞれ正孔と電子が伝導を担います.このとき,Sを測定するとそれぞれ+と-の値を示すことが知られています. 銅などの金属では負の電荷を持つ自由電子が電流担体ですが,バンド構造や電子のつまり方に応じて,正孔が電荷を運んでいると見なせる場合も生じます.このときSは+になります.ρは電気の流れやすさに関係しますが,Sを測定すると電気を運んでいる粒子についての情報を得ることができます. 以上のように,輸送係数の測定を組み合わせることで相補的な情報が得られます.また,輸送係数を温度や圧力を変化させたり,強磁場下で測定することで,その物質が金属なのか半導体なのかや,バンド構造についての詳細な知見が得られる場合もあります.ここで紹介した以外にも,ホール効果や磁気抵抗,ネルンスト効果を初めとした磁気熱電現象など様々な輸送現象が知られています.私たちのグループでは,低温・高圧・強磁場等の極限環境で種々の輸送係数を測定することによって新物質の物性解明を行っています. さらに詳しく知りたい方へ 固体・輸送現象の蔵書リスト |
